
La licorne dans les nuages avis et comment jouer
de lecture - mots
Glitterluck de la licorne : règles, revue et simulation de jeu

Dans notre famille, nous aimons jouer à des jeux de société avec nos enfants. Et les enfants aiment ça aussi. En particulier, ils aiment les jeux qui les font réfléchir à la stratégie et à ce qui se passe, tout en étant amusants. Pour le père geek que je suis, un jeu qui comporte des aspects non triviaux ajoute un bonus en me faisant poser des questions non évidentes (ce qui me divertit). Alors, quel est mon avis sur Unicorn Glitterluck : Cloud Crystals ?
Unicorn Glitterluck : Cloud Crystals est un jeu de société pour 2 à 4 joueurs âgés de 3 ans et plus. Le matériel de jeu est d'excellente qualité. L'issue du jeu est principalement déterminée par le lancer de dés, mais le jeu reste intéressant et amusant jusqu'à la fin et comporte plusieurs aspects éducatifs. Je le recommande vivement.
Mais ce n'est là que mon opinion rapide sur le jeu. Il y a un certain nombre de choses à son sujet qui méritent d'être partagées plus en détail, alors c'est parti :
Dans le jeu de société Unicorn Glitterluck : Cloud Crystals, 2 à 4 joueurs font la course à travers les nuages, lorsqu'ils essaient d'échapper à la pluie et d'atteindre le soleil. Mais ne font-ils que courir ? Non, ils collectent des cristaux en cours de route ! Et c'est ce qui compte vraiment, comme je l'explique ci-dessous, où je parle de ce qui permet de gagner le jeu.
Ce qu'il y a dans la boîte

La boîte de jeu contient :
- le plateau de jeu (photo ci-dessous), qui est assemblé à partir de trois grandes pièces de puzzle
- quatre figurines de licorne en boisOuverture d'un nouvel onglet. (voir photos ci-dessus et ci-dessous) de couleurs (et de noms) différentes
deux dés - Ouverture d'un nouvel onglet. (photos ci-dessous), un bleu avec des nuages, et un rose avec des cristaux
- un sac avec 60 cristaux en plastique rose (cette photo)
les instructions et le livre de règles du jeu (lien vers le pdf ci-dessous)
- Le matériel (planche, figures, cristaux) est de haute qualité. En particulier :
bien qu'elle soit assemblée à partir de trois pièces à chaque fois, la planche est stable et supporte bien les manipulations fréquentes des enfants - les licornes en bois ont le poids idéal pour jouer. Elles permettent également un jeu créatif en dehors des règles, comme l'empilage ou des idées similaires.
- les cristaux ont un beau design. En particulier, j'aime la forme, car les cristaux apparaissent facilement différents (en étant posés sur différentes parties de la surface), bien qu'ils soient tous exactement les mêmes.

Les règles
Je trouve les règles du jeu suffisamment simples pour que les enfants de 3 ans puissent les suivre, mais suffisamment complexes pour rendre le jeu intéressant et divertissant même pour les adultes. Voici les détails.
Le plateau de jeu de la Licorne Glitterluck : Cristaux de nuages

Le plateau de jeu présente le nuage foncé de départ dans le coin supérieur gauche, le nuage blanc d'arrivée dans le coin inférieur droit et, entre les deux, un certain nombre de nuages blancs, de nuages roses sur lesquels se trouve un dé et de nuages violets sur lesquels se trouve un cadeau. De plus, il y a trois arcs-en-ciel qui relient chacun deux des nuages.
Dés et mécanismes de jeu
Le jeu se joue en lançant des dés : les joueurs lancent à tour de rôle le dé bleu, qui comporte des petits nuages au lieu des points habituels. Si la licorne d'un joueur se déplace sur un nuage rose, il peut lancer le dé rose, qui comporte des petits cristaux à la place des points.

Le dé bleu à nuages a une face avec un maximum de trois nuages, deux faces avec deux nuages, deux faces avec un nuage et une face avec l'image d'un muffin. Le nombre de nuages indique au joueur combien de nuages sa licorne peut avancer sur le plateau en direction du nuage d'arrivée blanc. En revanche, s'il obtient un muffin, la licorne reste sur place (et mange le muffin), ce qui correspond à une valeur de zéro sur le dé. En termes de probabilités, il est deux fois plus probable d'obtenir un 1 ou un 2 que d'obtenir un 3 ou un 0.
Le fait que le nombre de nuages soit limité à un maximum de trois, et qu'il comprenne un zéro, donne un bon rythme de jeu. Étant donné qu'il faut 26 étapes pour arriver au nuage d'arrivée, un six sur ce dé accélérerait certainement trop le jeu et laisserait une grande partie du potentiel (collecte de cristaux) inexploitée....

Le dé de cristal rose a une face avec trois cristaux, deux faces avec deux cristaux, et trois faces avec un cristal. Un joueur lance le dé rose lorsqu'il arrive sur un nuage rose du plateau de jeu, et collecte le nombre de cristaux indiqué sur le dé. Ces cristaux sont ajoutés à la pile du joueur, qui représente le score réel dans le jeu (voir ci-dessous).
D'après la répartition des cristaux sur le dé, il est clair qu'il est plus probable de collecter un cristal, et que collecter trois cristaux à la fois n'arrive pas si souvent. Néanmoins, il est important que le nombre de cristaux augmente chaque fois qu'un joueur atterrit sur l'un des nuages roses.
Déménagements et événements spéciaux
Il y a quelques événements spéciaux et circonstances notables dans le jeu. Vous pouvez voir ceux qui sont liés au tableau dans l'image ci-dessus.
Les arcs-en-ciel : Ils servent de toboggans à sens unique. Une licorne qui atterrit sur le nuage au début de l'arc-en-ciel à la fin d'un mouvement doit glisser vers le nuage à la fin de l'arc-en-ciel. Et elle doit faire un bruit joyeux et sauter par-dessus la coccinelle, selon ma fille.

Cadeaux : Un joueur qui arrive sur l'un de ces nuages peut (et doit) donner un cristal à l'un des autres joueurs (et peut choisir lequel). Le cristal provient du réservoir de cristaux, et non de sa propre pile, donc c'est en fait quelque chose de très agréable à faire.
Bonus d'arrivée : La première licorne qui arrive à l'arrivée reçoit quatre cristaux bonus qui l'attendent.
Partage des nuages : Deux licornes ou plus peuvent partager le nuage sur lequel elles se trouvent. Personne ne doit retourner au départ pour quelque raison que ce soit dans le jeu.
Objectif du jeu et gagner le jeu
Le but du jeu est de collecter le plus de cristaux possible. Le gagnant est le joueur qui a collecté le plus de cristaux parmi tous les joueurs juste après le moment/mouvement où la première licorne arrive sur le nuage d'arrivée blanc et y collecte les quatre cristaux bonus.
Ainsi, le premier arrivé n'est pas toujours le gagnant. Bien qu'il soit utile de collecter les quatre cristaux bonus pour l'arrivée, il est beaucoup plus important de réussir à collecter des cristaux aussi souvent et aussi nombreux que possible pendant toute la partie. La question de savoir s'il est probable que la licorne qui termine ne gagne pas a été la première raison pour laquelle j'ai voulu faire une simulation de Monte-Carlo de ce jeu. Si vous êtes intéressé par la réponse à cette question et par d'autres statistiques sur ce qui peut arriver, jetez un coup d'œil à mon analyse ci-dessous.
Une idée géniale : Déterminer le gagnant sans compter
Il y a une autre chose intéressante à propos de ce jeu que je veux partager, c'est un moyen facile de déterminer le gagnant, même sans savoir compter. Cela peut être utile pour les très jeunes enfants qui jouent ainsi que pour d'autres idées visant à aider les enfants à apprendre à compter.
Au dos du plateau de jeu, il y a quatre lignes de nuages, une pour chaque licorne. Les figurines sont placées à leur emplacement, et les cristaux collectés sont disposés devant chacune d'elles, comme je le montre sur l'image. Ainsi, le gagnant est évident et il y a de nombreuses possibilités de jeux de comptage supplémentaires et d'autres idées.

Mes aspects préférés du jeu
Il y a une raison principale pour laquelle j'écris cette critique : J'ai personnellement trouvé une bonne dose de stimulation intellectuelle lorsque j'ai commencé à jouer à ce jeu et à réfléchir à toutes les issues possibles, etc. Mais ce n'est pas tout, j'aime aussi quelques autres choses en particulier. Les voici.
Le premier arrivé n'est pas automatiquement le vainqueurThe
Cet aspect est tout simplement génial. Il permet de maintenir l'intérêt de tous en évitant que les enfants ne perdent espoir parce qu'ils semblent toujours avoir des chiffres faibles. De plus, les enfants gardent constamment les scores en tête pour essayer de déterminer qui est en tête (car la position évidente sur le tableau n'est qu'une partie de l'équation).
The Present Clouds
Ces points dans le jeu permettent des moments de gentillesse, mais aussi de discuter des options, comme qui a le plus besoin d'aide, etc. Une touche très agréable pour le jeu.
S'amuser avec les muffins
Saviez-vous qu'il est amusant pour une figurine de licorne en bois de manger une image de muffin sur un dé ? Je ne le savais pas non plus, jusqu'à ce que je découvre que cela peut facilement faire comprendre aux enfants qu'ils viennent d'obtenir un zéro.
Unicorn Glitterluck Manufacturer’s Information
Avant que j'aille analyser le jeu à Monte-Carlo pour vous, voici les éléments les plus importants concernant le jeu et son fabricant :
- Nom : La licorne dans les nuages
- Nombre de joueurs : 2 à 4
- Âge recommandé des joueurs : 3 à 99 ans
- Durée d'une partie typique : 10 minutes
- Auteur : Kristin Mückel
- Illustrations : Stephanie Roehe
- Copyright : HAB
Ma recommandation
Un jeu de société parfait pour que les petits enfants apprennent et comprennent les mécanismes de jeu qui vont au-delà du simple fait de lancer un dé et d'avancer. En même temps, l'objectif semble fasciner les enfants, car ils ont besoin de comprendre d'où vient la victoire au lieu de simplement courir vers la ligne d'arrivée.
Si votre enfant aime les licornes, il n'y a pas grand-chose à redire, mais si ce n'est pas le cas, il y a un certain nombre de choses et de moments très sympathiques dans ce jeu. Je le recommande de tout cœur à toute famille aimant les jeux de société avec de jeunes enfants.
Pourquoi j'ai décidé de faire une simulation de Monte-Carlo de ce jeu.
Maintenant, amusons-nous un peu, d'accord ? Telles étaient mes pensées, lorsque j'ai décidé de faire une simulation de Monte-CarloOuverture d'un nouvel onglet. de Unicorn Glitterluck. Le point général d'une telle simulation est le suivant :
Les jeux de hasardOuverture d'un nouvel onglet. (comme les jeux de cartes ou les jeux de dés) peuvent être étudiés en utilisant la théorie des probabilitésOuverture d'un nouvel onglet. Pour chaque lancer de dé, par exemple, nous pouvons calculer très facilement la probabilité de chaque résultat. Cependant, lorsque nous concaténons un grand nombre de ces lancers avec le dé bleu et que nous souhaitons également calculer les résultats pour les différentes positions du plateau et les lancers du dé rose, en utilisant des diapositives arc-en-ciel, etc., cela devient beaucoup trop compliqué beaucoup trop rapidement.

La simulation de Monte-Carlo joue essentiellement des tas et des tas de jeux pour nous dans un ordinateur et nous donne les résultats de chacun d'eux. Ce qu'il est le plus utile de faire avec des simulations de ce type, c'est d'agréger des statistiques sur différents nombres d'intérêt. Voici quelques exemples :
- Combien de lancers de dés sont nécessaires pour terminer le jeu en moyenne ?
- Combien de cristaux le gagnant possède-t-il en moyenne ?
- Combien de cristaux sont collectés par toutes les licornes du jeu au total, en moyenne ?
- Combien de fois, en moyenne, le gagnant ne remporte-t-il pas la partie ?
- Quelle est la probabilité d'une égalité pour la première place ?
Simulation de Monte-Carlo du Glitterluck de la licorne : les cristaux des nuagesMonte-Carlo-Simulation of Unicorn Glitterluck: Cloud Crystals
J'ai programmé cette simulation de Monte-Carlo en pythonOpens in a new tab. en utilisant une installation standard avec les paquets numpyOpens in a new tab. et scipyOpens in a new tab. pour l'analyse ainsi que matplotlibOpens in a new tab. pour faire les graphiques.
Configuration de la simulation de Monte-Carlo
La configuration d'une simulation de Monte-Carlo comporte quelques paramètres importants. Le premier est le nombre d'échantillons à utiliser. Il s'agit en fait du nombre de groupes de parties que l'ordinateur doit jouer. Le second est la taille de l'échantillon, c'est-à-dire le nombre de parties de chaque groupe (échantillon) que l'ordinateur va jouer.
Pour ce cas particulier, j'ai lancé 50 échantillons de 1 million de parties chacun, ce qui est un nombre raisonnable (faites-moi confiance). Ils fournissent une précision suffisante sans coûter trop de temps à exécuter.
Questions intéressantes à poser
J'ai déjà noté ci-dessus un certain nombre de questions amusantes et intéressantes. Maintenant, nous allons examiner quelques réponses, enfin.
Nombre de cristaux du gagnant
Le nombre de cristaux que le gagnant de ce jeu a collecté en moyenne est de ... 11,47. Comment puis-je le savoir ? Tout d'abord, nous pouvons regarder n'importe quel échantillon particulier pour voir la distribution du nombre de cristaux du gagnant depuis le nombre minimal de 4 jusqu'à 20 et au-delà (du moins en théorie, mais les probabilités deviennent très faibles très rapidement). La voici :
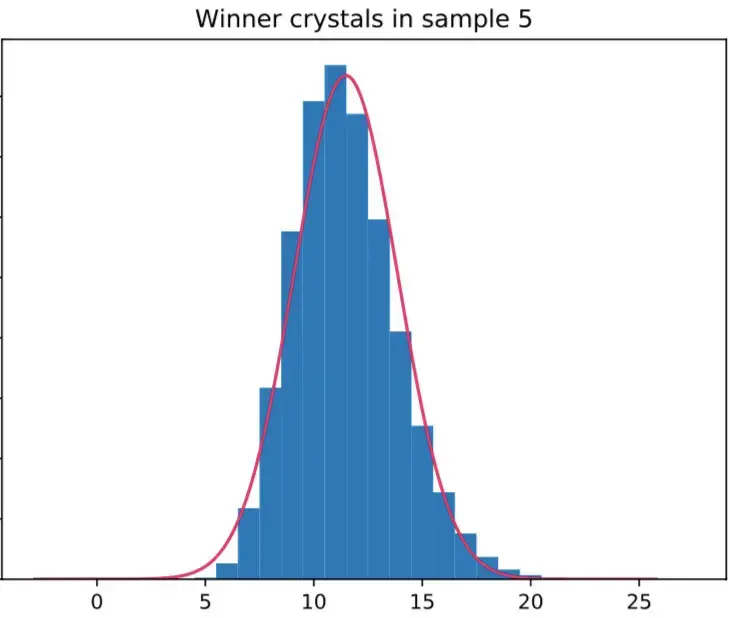
Les barres bleues indiquent la quantité relative de résultats de jeu pour lesquels le gagnant avait le nombre de cristaux noté sur l'axe horizontal inférieur, ce qui s'appelle une distribution de probabilité. La courbe rose est un ajustement gaussien des données, qui, apparemment, ne sont pas tout à fait gaussiennes (normalement distribuées), mais suffisamment proches pour que la courbe soit là.
D'après la barre la plus haute et le sommet de la courbe, nous pouvons voir que le maximum se situe entre 11 et 12, mais nous ne savons pas où exactement. Et c'est ici que les différents échantillons entrent en jeu. À partir de la collection d'échantillons, nous pouvons créer une autre figure qui nous donne la distribution du nombre que nous observons (le pic de la courbe), tracée à travers les échantillons. Voici à quoi cela ressemble :
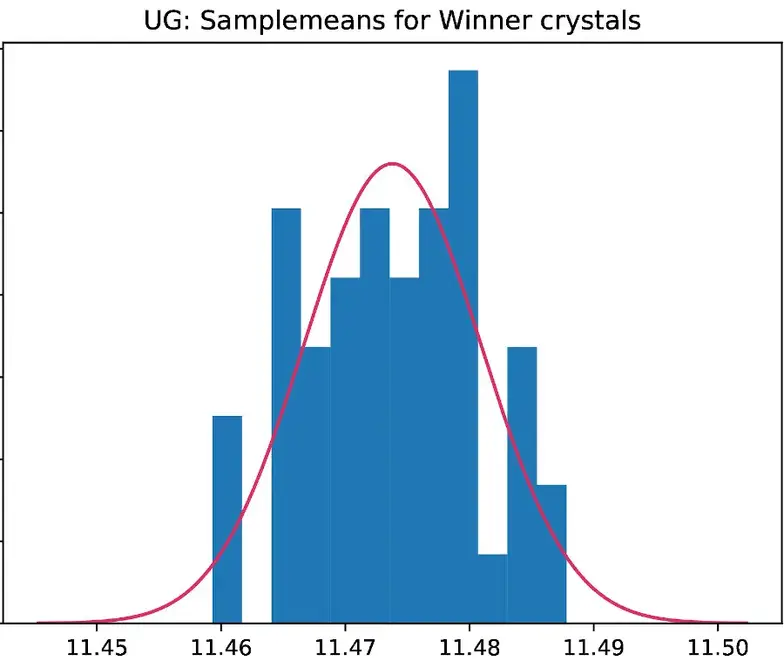
À partir de ce graphique, nous pouvons maintenant voir d'où vient le nombre moyen que j'ai cité plus haut. Les mêmes principes peuvent être appliqués à d'autres chiffres intéressants, dont quelques-uns sont présentés ci-dessous.
Nombre total de cristaux collectés par tous les joueurs
Distribution de probabilité du nombre total de cristaux dans l'un des échantillons de ma simulation Monte-Carlo du Glitterluck de la Licorne.
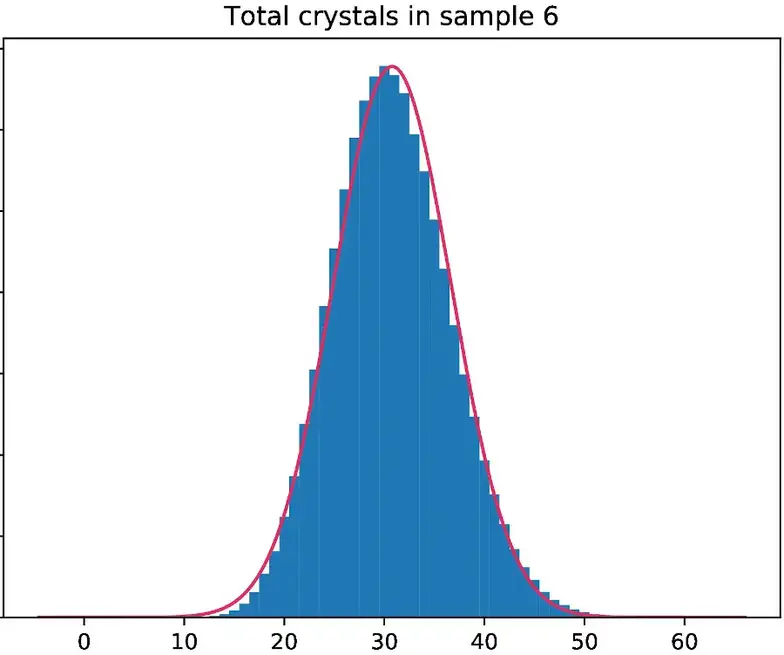
Il ne reste pas grand-chose de la probabilité au-delà de 55 cristaux au total, donc je doute que nous soyons à court de cristaux dans un jeu réel de sitôt. Si vous voulez un chiffre concret sur la fréquence à laquelle le nombre total de cristaux a dépassé 60 dans mes échantillons, voici : une poignée sur un million.
À propos, le minimum théorique (et pratique) du nombre total de cristaux dans une partie est de 5. Pouvez-vous comprendre pourquoi, en regardant le plateau de jeu ci-dessus ?
Et pour être complet : Le nombre moyen cité ci-dessus provient à nouveau des moyennes de l'échantillon, mais je ne veux pas vous ennuyer, nous passons donc à la question suivante :
Traduit avec www.DeepL.com/Translator (version gratuite)
Combien de fois le premier arrivé ne gagne-t-il pas ?
C'est vraiment intéressant. Alors qu'une des licornes peut courir rapidement mais sauter tous les nuages roses et ainsi se retrouver avec seulement 4 cristaux à la fin du plateau de jeu, les autres peuvent s'arrêter à chaque nuage rose et collecter des cristaux comme des fous, et ainsi gagner facilement. Ok, maintenant nous voyons comment c'est possible, mais quelle est la probabilité ?
La réponse à la question de savoir combien de fois le finisseur gagne également la partie est ... 78,5 %. Ainsi, dans plus de 20 % des parties, le gagnant est l'une de ces licornes qui ne terminent pas en premier.
Traduit avec www.DeepL.com/Translator (version gratuite)






















